设计模式
设计模式随笔
最近复习下设计模式,顺便写下随笔
设计模式的六大原则
单一职责原则 英文:single responsibility principle,缩写:SRP
单一职责就是一个借口或类,只完成一个职责
好处: 类的复杂性降低、可读性提高、可维护性提高、降低变更引起的风险里式替换原则
官方定义:所有引用基类的地方必须能透明的使用其子类对象
简单的说,就是父类使用的地方,都能用子类替换依赖倒置原则
定义:- 高层模块不应该依赖底层模块,两者都应该依赖期抽象
- 抽象不应该依赖细节
- 细节应该依赖抽象
不可分割的原子逻辑就是底层模块,原子逻辑再组装就是高层模块,java中,抽象就是借口或抽象类,细节就是实现类,也就是new 出来的对象
最精简的定义:面向接口编程
采用依赖倒置原则可以减少类间的耦合性,提高系统的稳定性,降低并行开发引起的风险,提高代码的可读性和可维护性
接口隔离原则
定义: 客户端不应该依赖它不需要的接口,类间的依赖关系应建立在最小接口上
简单来说就是建立单一接口,功能细化,不要臃肿,不要去实现不必要的接口
迪米特法则,law of demeter lod,也成最少知识原则(least knowlege priciple lkp)
一个对象应该对其他对象有对少的了解
通俗说,一个类不关心耦合类的内部接口,只关心耦合类暴露的方法
核心:高内聚,低耦合
开闭原则
定义: 一个软件实体,如类、模块和函数,应该对扩展开放,对修改关闭简单来说,通过新增类扩修改业务代码进行扩展,而非修改功能性代码。
23种设计模式
单例模式
定义:确保某一个类只有一个实例,且自行实例化冰箱整个系统提供这个实例工厂方法模式
定义: 定义一个用于创建对象的接口,让子类决定实例化哪一类,工厂方法使用一个类的实例化延迟到其子类
抽象工厂模式
定义: 为创建一组相关或相互依赖的对象提供一个接口,而且无需指定他们的具体类模板方法模式
定义:定义一个操作中的算法的框架,将一些步骤延迟到子类中。使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤
建造者模式
定义:将一个复杂对象的构建与它的表示分离,使得同样的构建过程可以创建不同的表示
代理模式
定义: 为其他对象提供一种代理以控制对这个对象的访问
7. 原型模式
定义: 用原型示例指定创建对象的种类,并且通过拷贝这些原型创建新的对象
java中jdk自带的clone就是
优点: 对象的创建时内存二进制流的拷贝,性能比new对象好
- 中介者模式
定义: 用一个中介对象封装一系列的对象交互,中介者使各对象不需要显示的相互作用,从而使其耦合松散,,而且可以独立的改变他们之间的交互
- 命令模式
定义:将一个请求封装成一个对象,从而让你使用不同的请求把客户端参数化,对请求排队或者记录请求日志,可以提供命令的撤销和恢复功能
- 责任链模式
定义:使多个对象都有机会处理请求,从而避免了请求的发送者和接受者之间的耦合关系。将这些对象连城一条链,并沿着这条链传递该请求,知道有对象处理它为止。
- 装饰模式 decorator pattern
定义:动态的给一个对象添加一些额外的职责。就增加功能来说,装饰模式相比生成子类更为灵活
优点:
1. 装饰类和被装饰类可以独立发展,而不会互相耦合
2. 装饰模式是集成关系的一个替代方案
3. 装饰模式可以动态的扩展一个实现类的功能
缺点:剁成的装饰是复杂的
使用场景:
1. 需要扩展一个类的功能,或者给一个类增加附加功能
2. 需要动态的给一个对象增加功能,这些功能可以动态的撤销
3. 需要为一批的兄弟类进行改装或加装功能
- 策略模式 strategy pattern
定义:定义一组算法,将每个算法都封装起来,并且使它们之间可以互换
优点:
- 算法可以自由切换
- 避免使用多重条件判断
- 扩展性良好
缺点:
- 策略类数量增多
- 所有的策略类都需要对外暴露
使用场景:
- 多个类只有在算法或行为上稍有不同的场景
- 算法需要自由切换的场景
- 需要屏蔽算法规则的场景
- 适配器模式 adapter pattern
- 定义:将一个类的接口变换成客户端所期待的另一种接口,从而使原本因接口不匹配而无法在一起工作的两个类能够在一起工作
- 优点:
- 适配器模式可以让两个没有任何关系的类在一起运行,只要适配器这个角色能够搞定他们就成
- 增加了类的透明性
- 提高了类的复用度
- 灵活性非常好
- 缺点:
- 使用场景:后期修改一个接口或类
- 迭代器模式 iterator pattern
- 定义:它提供一种方法访问一个容器对象中各个元素,而又不需暴露该对象的内部细节
- 优点:
- 缺点:
- 使用场景:
- 组合模式
- 定义:
- 优点:
- 高层模块调用简单
- 节点自由增加
- 缺点:
- 使用场景:维护和展示部分-整体关系的场景
- 观察者模式 observer pattern
- 定义:定义对象间一种一对多的依赖关系,使得每当一个对象改变状态,则所有依赖于它的对象都会得到通知并被自动更新
- 优点:
- 观察者和被观察之间是抽象耦合
- 建立一套触发机制
- 缺点:
- 使用场景:
- 门面模式 facade pattern
定义:要求一个子系统的外部与其内部的通信必须通过一个统一的对象进行。门面模式提供一个高层次的接口,使得子系统更易于使用。
优点:
- 减少系统的相互依赖
- 提高灵活性
- 提高安全性
缺点:
使用场景:
- 为一个复杂的模块或子系统提供一个供外界访问的接口
- 子系统相对独立——外界对子系统的访问只要黑箱操作即可
- 备忘录模式
- 定义:
- 优点:
- 缺点:
- 使用场景:
- 访问者模式 visitor pattern
- 定义:封装一些作用于某种数据结构中的各元素的操作,它可以在不改变数据结构的前提下定义作用于这些元素的新的操作。
- 优点:
- 符合单一职责远侧
- 优秀的扩展性
- 灵活性高
- 缺点:
- 具体元素对访问者公布细节
- 具体元素变更比较困难
- 违背了依赖倒置原则
- 使用场景:
- 状态模式 state pattern
定义:当一个对象内在状态改变时允许其改变行为,这个对象看起来像改变了其类
优点:
- 结构清晰
- 遵循设计原则
- 封装性非常好
缺点:子类太多
使用场景:
- 行为随状态改变而改变的场景
- 条件、分支判断语句的替代者
- 解释器模式 intrpreter pattern
- 定义:给定一门语言,定义它的文法的一种表示,并定义一个解释器,该解释器使用该表示来解释语言中的句子
- 优点:
- 缺点:
- 解释器模式会引起类膨胀
- 采用递归调用方法
- 效率问题
- 使用场景:
- 享元模式 flyweight pattern
- 定义:使用共享对象可有效地支持大量的细粒度的对象
- 优点:
- 缺点:
- 使用场景:
- 系统中存在大象的相似对象
- 细粒度的对象都具备较接近的外部状态,而且内部状态与环境无关
- 需要缓冲池场景
- 桥梁模式 bridge pattern
- 定义:将抽象和实现解耦,使得两者可以独立地变化
- 优点:
- 抽象和实现分离
- 优秀的扩充能力
- 实现细节对客户透明
- 缺点:
- 使用场景:
- 不系统或不适用继承的场景
- 接口或抽象类不稳定的场景
- 重要性要求较高的场景
hexo next 调整字体大小
今天在调整个人博客时,发现字体偏大
看着挺不舒服的,就想把字体调小一点。
搜索了一圈,发下next下有现成的配置。
在/them/next/_config.yml下,顺利的找到了调整的地方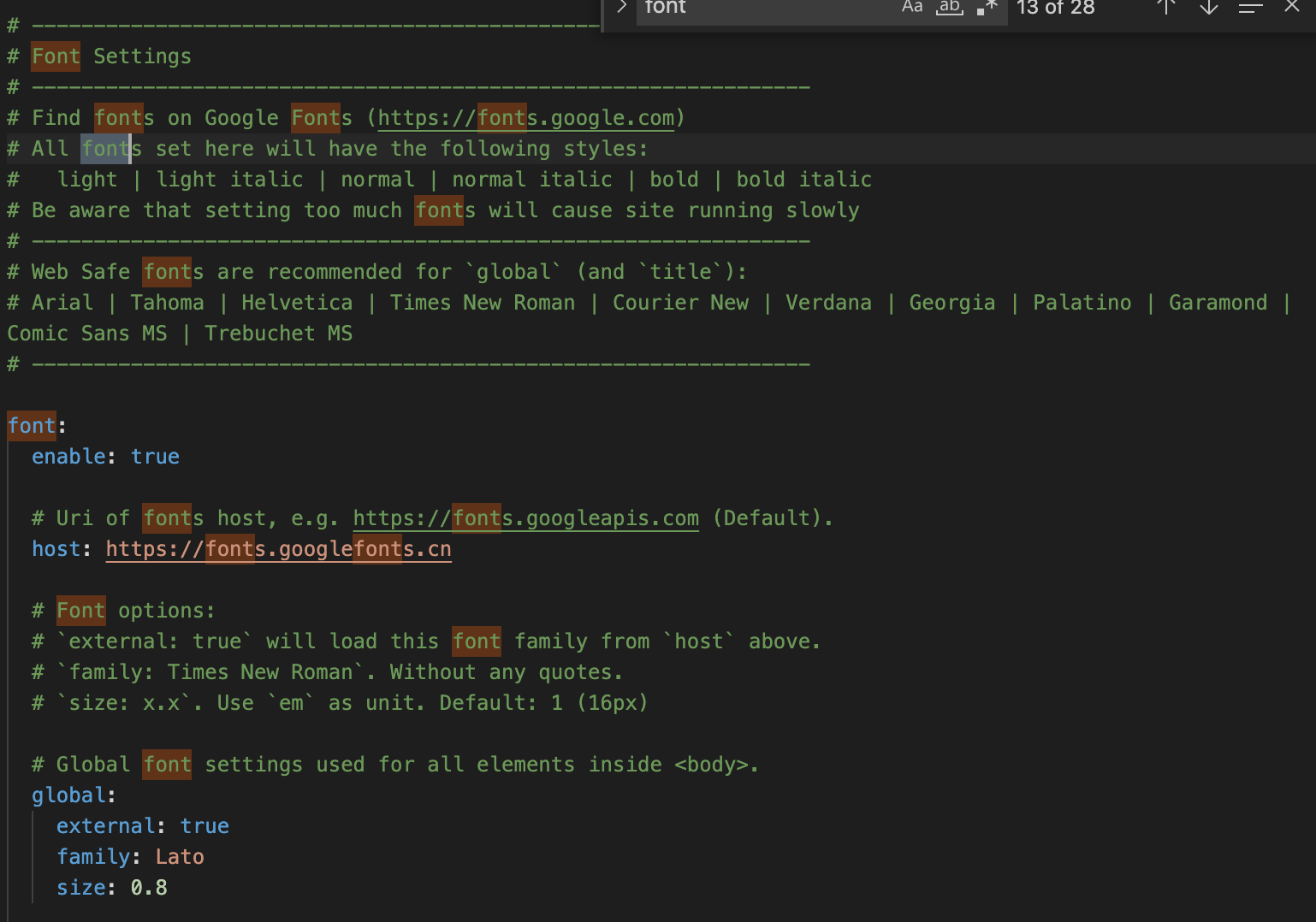
1、将font下enable改为true,表示开启字体下载2、将host设置为 https://fonts.googlefonts.cn 表示从哪个网站下载
2、将host设置为 https://fonts.loli.net 表示从哪个网站下载
系统默认的是 https://fonts.google.com ,然而由于国内的原因,你懂得,无法连接,万幸的是,有谷歌字体国内版:https://www.googlefonts.cn/ ,我们只要把host改成国内版即可
我们需要一些国内站替换或cdn,经过本人搜索,css.loli.net提供了国内对应谷歌的一些服务
1 | ajax.googleapis。com -> ajax.loli.net |
3、将global的size调整为0.8
调整完后,这字体就非常的舒适了。
spark源码阅读准备:使用 idea remote debug + sbt debug spark源码单元测试
背景
阅读spark源码时,从spark的单元测试入手是一个非常好的选择,spark的单元测试覆盖了非常多的场景,从单元测试入手非常有助于我们理解spark原理。
如:BroadcastSuite中的
1 | encryptionTest("Cache broadcast to disk") { conf => |
非常简单易懂,从字面意思我们就能理解这个单元测试是做什么的,那么如何debug呢?这就开启我们的debug之旅。
基本原理
采用java jdwp(Java Debug Wire Protocol) 实现,也就是远程debug,它定义了调试器(debugger)和被调试的 Java 虚拟机(target vm)之间的通信协议。
想要具体了解,可以参考此篇 使用jdwp远程debug java代码
我们采用idea作为服务器listner,spark sbt单元测试作为客户端的方式进行debug。
具体操作
idea remote debug listner开启
1、点击run下的edit configuration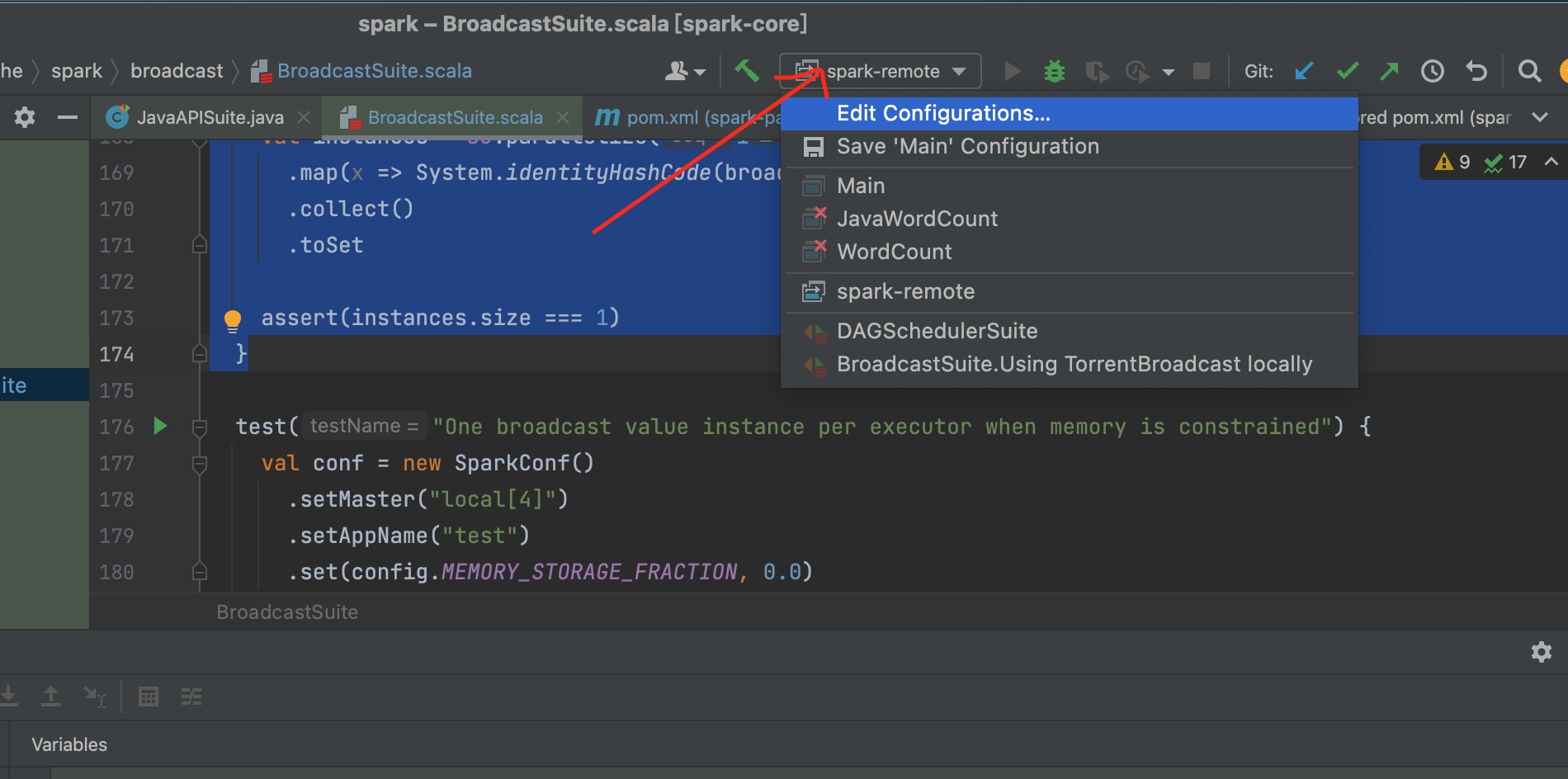
2、配置remote debug,具体如下图所示
端口这些一般使用默认的就好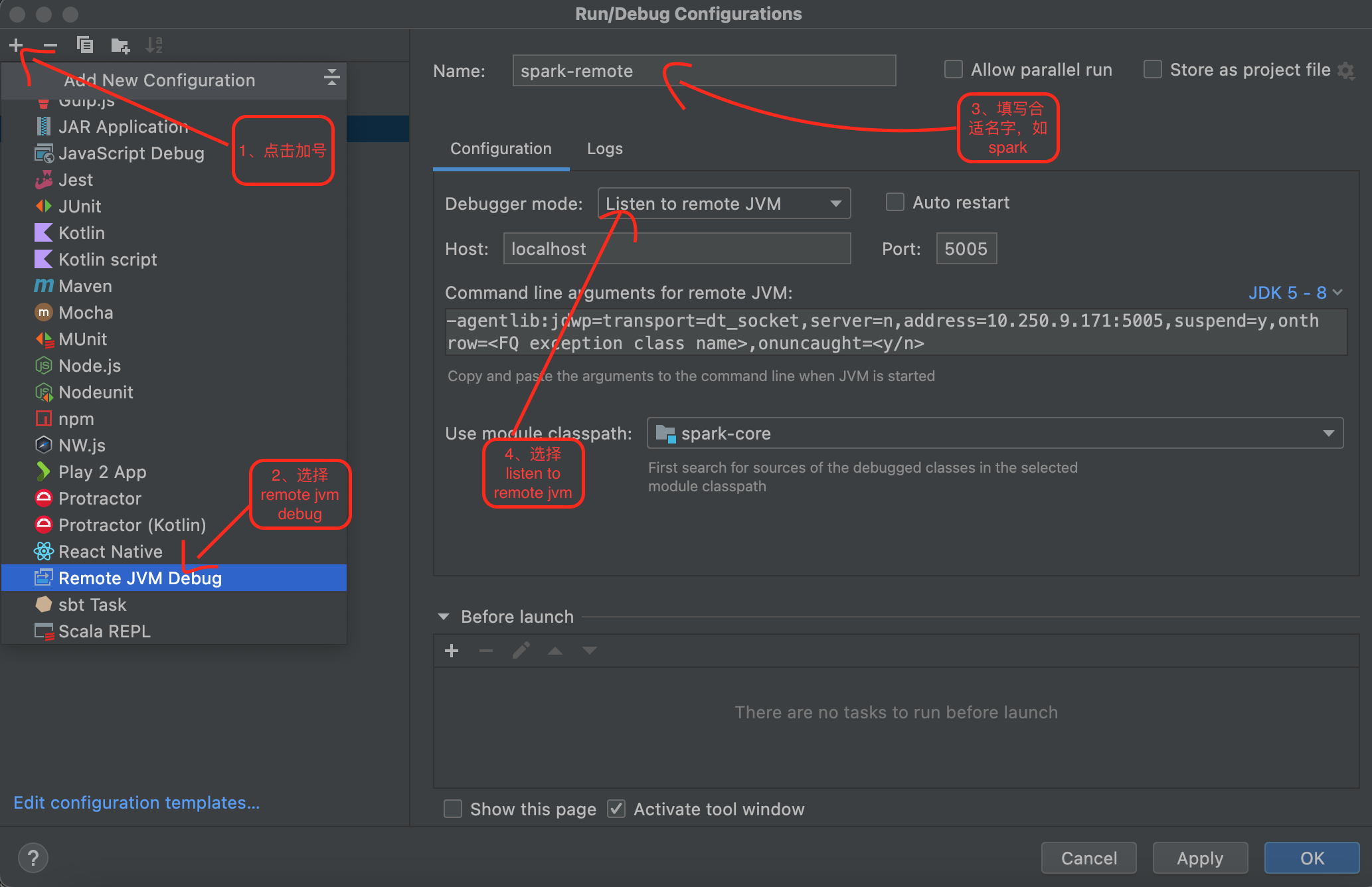
3、点击debug按钮,启动remote debug listner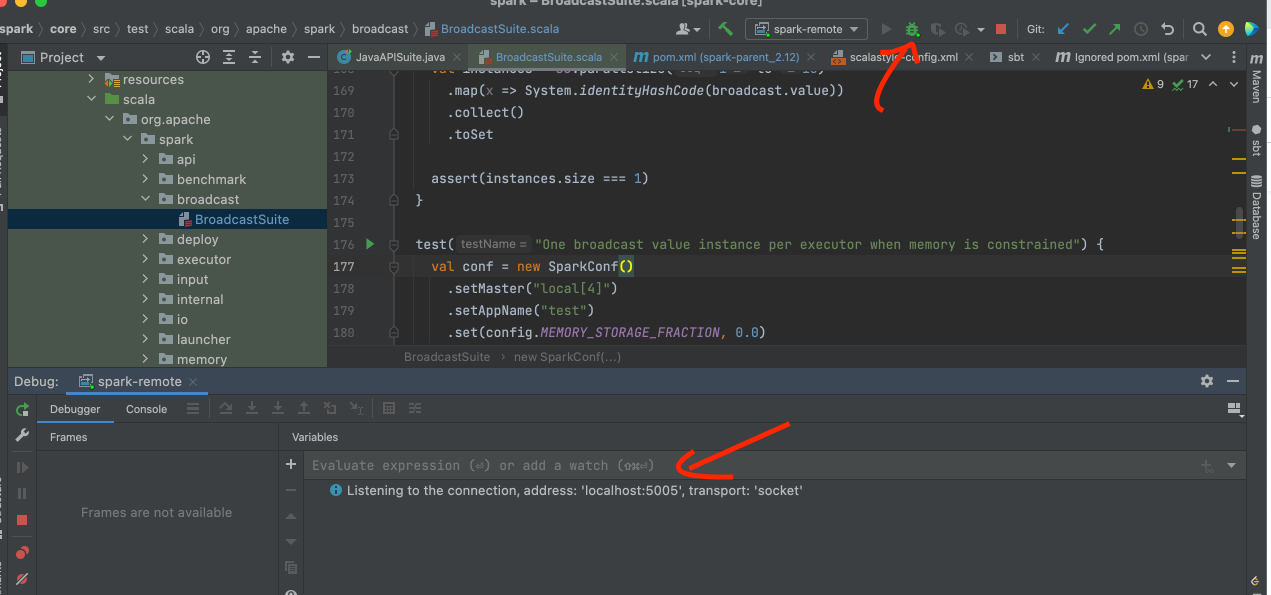
SBT 操作
基于sbt,我们可以运行spark的单元测试,在运行我们设置好jvm参数即可链接上idea的remote debug listner,下面以运行spark core项目下的BroadcastSuite下的 test("Using TorrentBroadcast locally") 为例
1、进入spark目录
2、运行./build/sbt ,启动spark自带的sbt server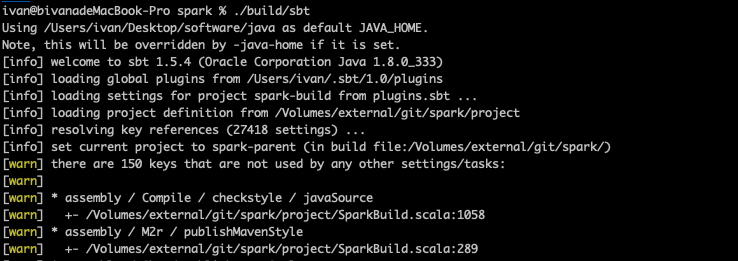

此时,sbt server启动完毕,可以看到我们在spark-parent总的项目下
3、输入 project core ,切换到spark core 子module下
4、输入
1 | set javaOptions in Test += "-agentlib:jdwp=transport=dt_socket,server=n,suspend=y,address=localhost:5005" |
表示运行单元测试时,启动jvm代理,连接到本地5005端口,也就是上文idea启动的监听端口
5、运行单元测试
1 | testOnly *BroadcastSuite -- -z "Using TorrentBroadcast locally" |
其中,-z 后面的参数为scala test后面跟的字段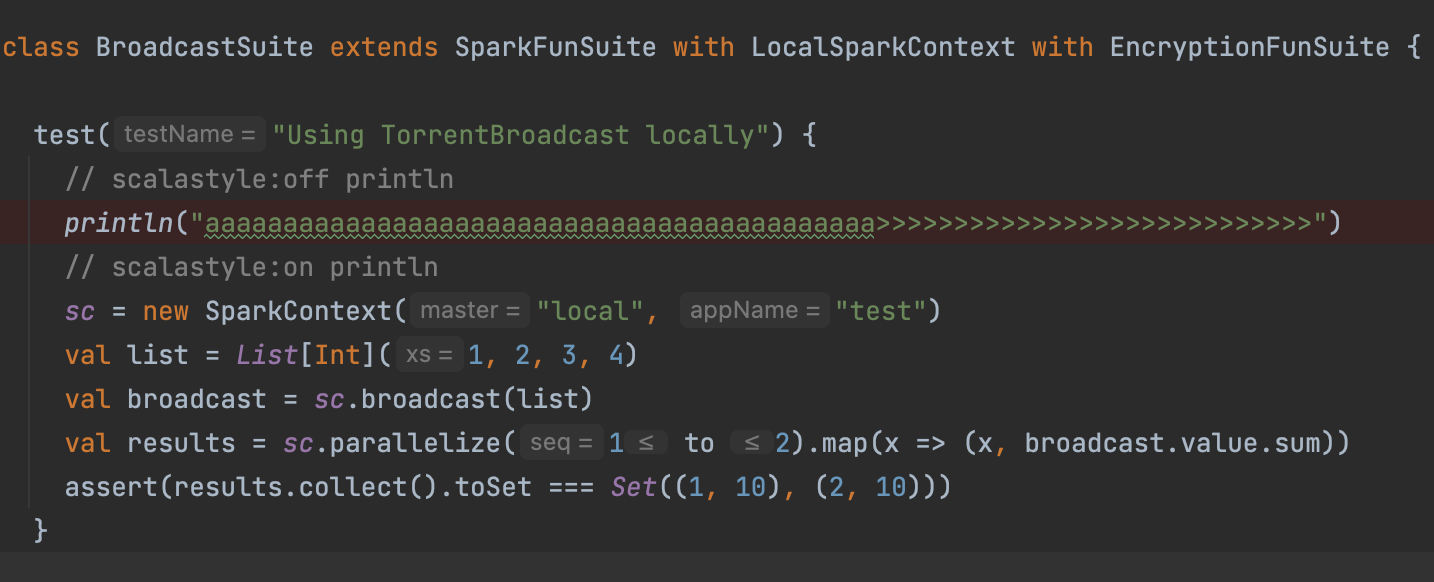
运行结果如下图所示: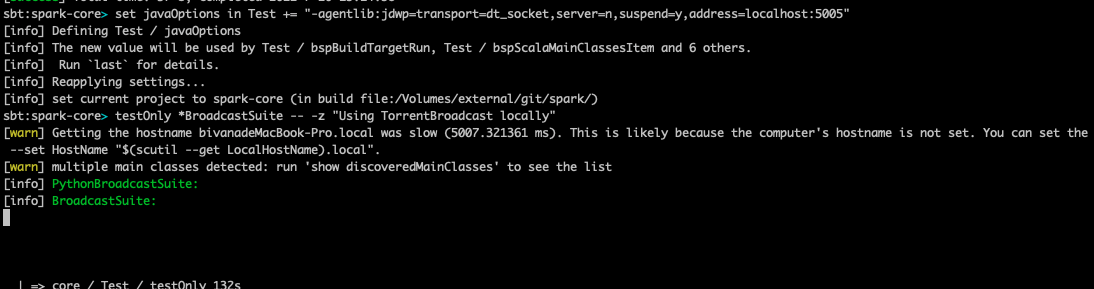
可以看到,单元测试运行到broadcastSuit时被阻塞,这是因为我们在idea断debug了。
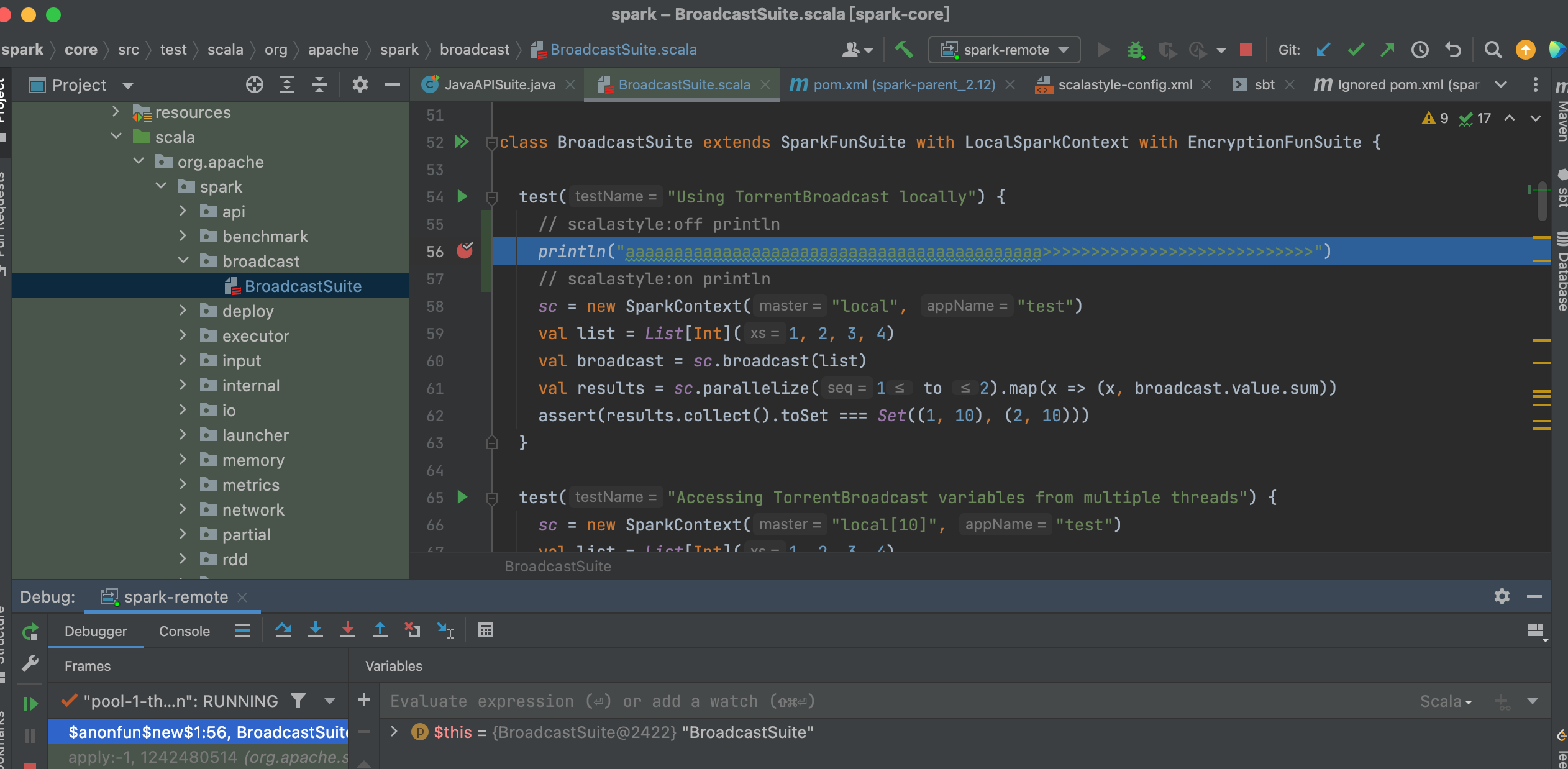
可以看到,idea的spark源码已经顺利进入断点模式,可以愉快的debug spark源码了,祝大家阅读源码愉快。
参考资料
使用jdwp远程debug java代码
本文转自 ieda-远程调试(java -agentlib:jdwp)
背景
当项目投产后,可能会遇到之前测试环境上没有遇到的问题,而又无法快速定位问题原因,令人十分捉急。
如果开发人员电脑可以接入生产环境,则可以采用java -agentlib:jdwp命令、idea或eclipse进行远程调试。
本文中使用IDEA进行远程调试。
#概念介绍
-agentlib 是什么
agentlib表示加载本机的代理库,输入java命令后,可以看到agentlib的介绍
1 | -agentlib:<libname>[=<选项>] |
JDWP 是什么?
JDWP 是 Java Debug Wire Protocol 的缩写,它定义了调试器(debugger)和被调试的 Java 虚拟机(target vm)之间的通信协议。
当使用java -agentlib:jdwp启动jar时,表示也在会address对应的端口上启动一个tcp监听,等待客户端(调试端,比如idea、eclipse)连接。
1 |
|
远程debug操作
操作可以分为2类
1、idea作为服务,等待客户端连接
2、其他java进程作为服务,等待idea客户端连接
本文采用方式2
服务端配置
服务端启动jar命令,增加java -agentlib:jdwp,如下:
1 | # 需要保证-agentlib:jdwp命令在 -jar命令之前 |
客户端idea配置
使用的是idea remote jvm debug功能,如下图所示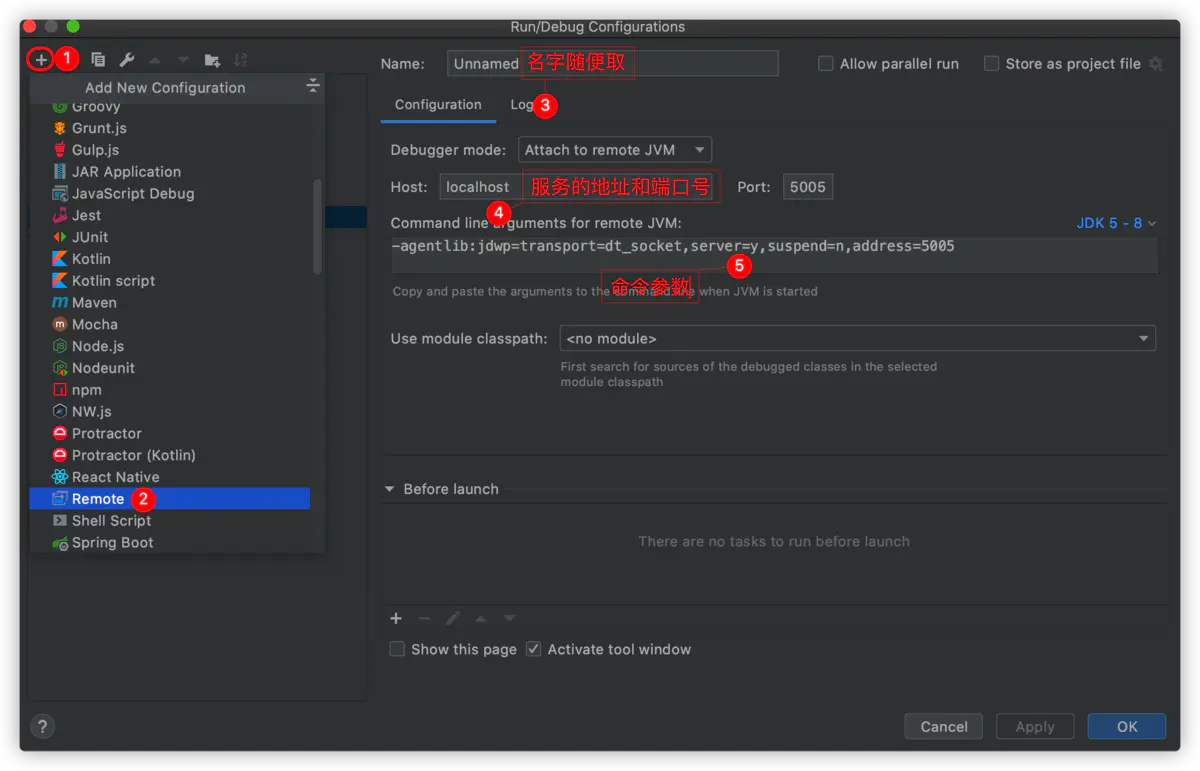
启动调试
1、启动jar
2、在idea中启动配置好的Remote
3、在源码中打断点,就可以调试
另Arthas很强大,也可以使用Arthas进行线上调试。
线段树
本文转自线段树可以解决什么问题
线段树概述
线段树是什么?
线段树是一种高级数据结构,也是一种树结构,准确的说是二叉树。它能够高效的处理区间修改查询等问题。因此学习线段树,我们就是在学习一种全新的高级数据结构,学习它如何组织数据,然后高效的进行数据查询,修改等操作。
线段树树的基本操作有哪些?
- 线段树的构建
- 线段树的修改
- 线段树的查询
这些基本操作都会在后面部分讲到。
线段树的使用场景?
- 用于维护区间信息(要求满足结合律)
- 实现 [公式] 的区间修改
- 持多种操作(加、乘),更具通用性
线段树问题举例
我们有时会遇到这样的问题: 给你一些数,组成一个序列,如[1 4 2 3],有两种操做: 操作一:给序列的第i个数加上X (X可以为负数) 操作二:询问序列中最大的数是什么? 格式query(start, end),表示区间[start, end]内,最大值是多少?
思路解析
我们很容易得到一个朴素的算法: 将这些数存入一个数组, 由于要询问最大值, 我们只需要遍历这个区间[start, end]即可,找出最大值。 对于改变一个数, 我们就在这个数上加上X,比如A[i] = A[i] + X。 这个算法的缺点是什么呢?Query询问最大值复杂度O(N), 修改复杂度为O(1),在有Q个query的情况下这样总的复杂度为O(QN), 那么对于查询来说这样的复杂度是不可以接受的,太高了!然后我们开始优化,如果你没有学过线段树,那么对于这个问题的优化是很难做的,甚至毫无头绪,基本上无从无从入手。
如果你学习了线段树,这个问题很容易解决,线段树就是一把区间问题解决的利刃,很多没有头绪的区间查询,修改问题都可以使用线段树解决。 那么这道题线段树应该怎么做?希望大家带着疑问阅读线段树的入门教程。
线段树的结构
首先线段树是一棵二叉树, 平常我们所指的线段树都是指一维线段树。 故名思义, 线段树能解决的是线段上的问题, 这个线段也可指区间. 我们先来看线段树的逻辑结构。
一颗线段树的构造就是根据区间的性质的来构造的, 如下是一棵区间[0, 3]的线段树,每个[start, end]都是一个二叉树中的节点。
1 | [0,3] |
区间划分大概就是上述的区间划分。可以看出每次都将区间的长度一分为二,数列长度为n,所以线段树的高度是log(n),这是很多高效操作的基础。 上述的区间存储的只是区间的左右边界。我们可以将区间的最大值加入进来,也就是树中的Node需要存储left,right左右子节点外,还需要存储start, end, val区间的范围和区间内表示的值。
1 | [0,3] |
区间的第三维就是区间的最大值。 加这一维的时候只需要在建完了左右区间之后,根据左右区间的最大值来更新当前区间的最大值即可,即当前子树的最大值是左子树的最大和右子树的最大值里面选出来的最大值。
因为每次将区间的长度一分为二,所有创造的节点个数,即底层有n个节点,那么倒数第二次约n/2个节点,倒数第三次约n/4个节点,依次类推:
1 | n + 1/2 * n + 1/4 * n + 1/8 * n + ... |
所以构造线段树的时间复杂度和空间复杂度都为O(n)
二叉树的节点区间定义,[start, end]代表节点的区间范围,max 是节点在[start, end]区间上的最大值 left , right 是当前节点区间划分之后的左右节点区间
1 | // 节点区间定义 |
线段树区间最大值维护
给定一个区间,我们要维护线段树中存在的区间中最大的值。这将有利于我们高效的查询任何区间的最大值。给出A数组,基于A数组构建一棵维护最大值的线段树,我们可以在O(logN)的复杂度内查询任意区间的最大值:
比如原数组 A = [1, 4, 2, 3]
1 | [0,3] |
1 | // 构造的代码及注释 |
举一反三: 如果需要区间的最小值: root.min = Math.min(root.left.min, root.right.min); 如果需要区间的和: root.sum = root.left.sum + root.right.sum;
线段树的区间查询
1. 如何更好的查询Query
构造线段树的目的就是为了更快的查询。
给定一个区间,要求区间中最大的值。线段树的区间查询操作就是将当前区间分解为较小的子区间,然后由子区间的最大值就可以快速得到需要查询区间的最大值。
1 | [0,3] |
1 | query(1,3) = max(query(1,1),query(2,3)) = max(4,3) = 4 |
上述例子将[1, 3]区间分为了[1, 1]和[2, 3]两个区间,因为[1, 1]和[2, 3]存在于线段树上,所以区间的最大值已经记录好了,所以直接拿来用就可以了。所以拆分区间的目的是划分成为线段树上已经存在的小线段。
2. 如何拆分区间变成线段树上有的小区间:
在线段树的层数上考虑查询 考虑长度为8的序列构造成的线段树区间[1, 8], 现在我们查询区间[1, 7]
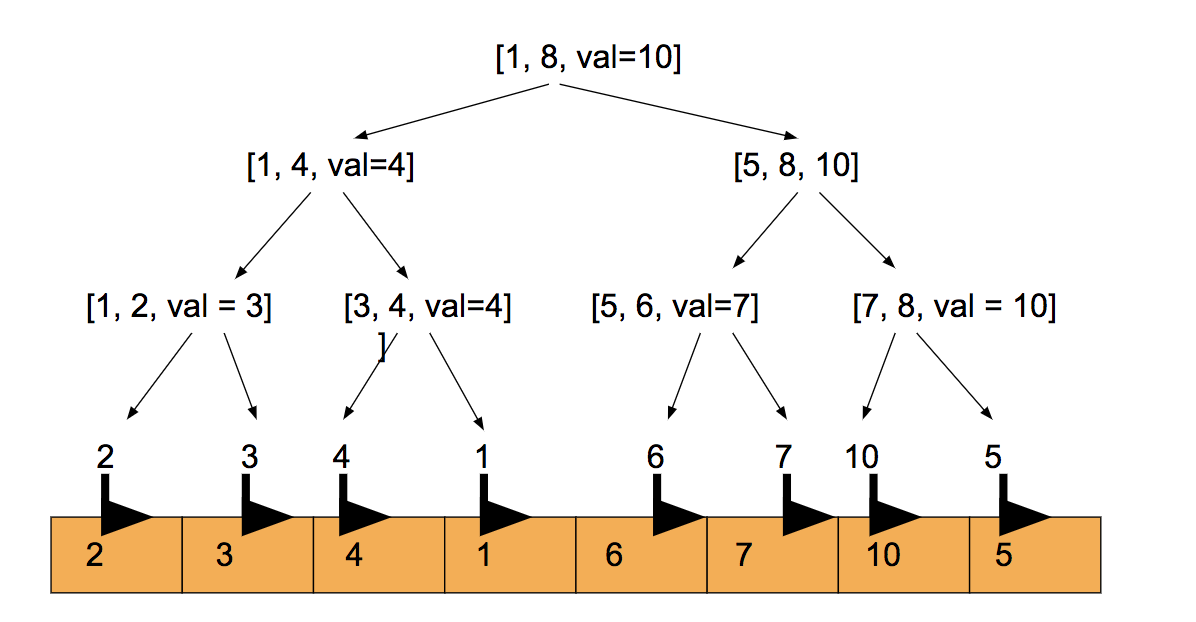
第一层会查询试图查询[1, 7], 发现区间不存在,然后根据mid位置拆分[1, 4]和[5, 7] 第二层会查询[1, 4],[5, 7], 发现[1, 4]已经存在,返回即可,[5, 7]仍旧需要继续拆分 第三层会查询[5, 6],[7, 7], 发现[5, 6]已经存在,返回即可,[7, 7]仍旧需要继续拆分 第四层会查询[7, 7]
任意长度的线段,最多被拆分成logn条线段树上存在的线段,所以查询的时间复杂度为O(log(n)) 记住就好:)
1 | // 区间查询的代码及注释 |
线段树的单点更新
1. 更新序列中的一个点
1 | [0,3] |
更新序列中的一个节点,如何把这种变化体现到线段树中去,例如,将序列中的第4个点A[3]更新为5, 要变动3个区间中的值,分别为[3,3],[2,3],[0,3]
提问:为什么需要更新这三个区间?:因为只有这三个在线段树中的区间,覆盖了3这个点。
1 | [0,3] |
1 | (val=1)(val=4) (val=2)(val=5) |
可以这样想,改动一个节点,与这个节点对应的叶子节点需要变动。因为叶子节点的值的改变可能影响到父亲节点,然后叶子节点的父亲节点也可能需要变动。
如果我们继续把A[2]从2变成4,线段树又该如何更新呢? 线段树变化后的状态为:
1 | [0,3] |
1 | (val=1)(val=4) (val=4)(val=5) |
如果我们继续把A[1]从4变成3,线段树又该如何更新呢? 线段树变化后的状态为:
1 |
|
1 | (val=1)(val=3) (val=4)(val=5) |
更新所以需要从叶子节点一路走到根节点, 去更新线段树上的值。因为线段树的高度为log(n),所以更新序列中一个节点的复杂度为log(n)。 因为每次从父节点走到子节点的时候,区间都是一分为二,那么我们要修改index的时候,我们从root出发,判断index会落在左边还是右边,然后继续递归,这样就可以很容易从根节点走到叶子节点,然后更新叶子节点的值,递归返回前不断更新每个节点的最大值即可。具体代码实现如下:
1 | // 单点更新的代码及注释 |
如果需要区间的最小值或者区间的和,构造的时候同理。
线段树模板-线段树动态开点
动态开点的线段树节点
1 | /** |
动态开点的更新
1 | /** |
动态开点的查询
1 |
|
实战面试题
实战面试题1 - 731. 我的日程安排表 II
leetcode原题:https://leetcode.cn/problems/my-calendar-ii/
题目大意:
1 | 实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内不会导致三重预订时,则可以存储这个新的日程安排。 |
解题思路:
标准的区间求最大值,直接套用模板
题解:
1 | class MyCalendarTwo { |
问题集
技术问题
股票
从哪下载上市公司财报
证监会 指 中国证券监督管理委员会
中核集团 指 中国核能电力股份有限公司控股股东,中国核工业集团有限公司
公司、本公司、
中国核电 指 中国核能电力股份有限公司
秦山核电 指
秦山核电有限公司、核电秦山联营有限公司和秦山第三核电有限公
司三家公司的简称
秦山一核 指
秦山核电有限公司,原秦山核电公司,为本公司直接持有 72%股权的
控股子公司
秦山二核 指 核电秦山联营有限公司,为本公司直接持有 50%股权的控股子公司
秦山三核 指 秦山第三核电有限公司,为本公司直接持有 51%股权的控股子公司
方家山核电 指 秦山核电有限公司所属的秦山核电厂扩建项目
田湾核电 指 江苏核电有限公司,为本公司直接持有 50%股权的控股子公司
三门核电 指 三门核电有限公司,为本公司直接持有 56%股权的控股子公司
福清核电 指 福建福清核电有限公司,为本公司直接持有 51%股权的控股子公司
海南核电 指 海南核电有限公司,为本公司直接持有 51%股权的控股子公司
漳州能源 指
中核国电漳州能源有限公司,为本公司直接持有 51%股权的控股子公
司
辽宁核电 指 中核辽宁核电有限公司,为本公司直接持有 54%股份的控股子公司
中核苏能 指 中核苏能核电有限公司,为本公司直接持有 51%股权的控股子公司
桃花江核电 指
湖南桃花江核电有限公司,为本公司直接持有 51.16%股权的控股子
公司
中核汇能 指 中核汇能有限公司,为本公司直接持有 100%股权的控股子公司
中核燕龙 指 中核燕龙科技有限公司,为本公司直接持有 51%股权的控股子公司
中核武汉 指
中核武汉核电运行技术股份有限公司,为本公司直接和间接持有
55.72%股权的控股子公司
华龙一号 指
中国拥有完全自主知识产权的三代压水堆技术,采用“能动与非能
动”相结合的安全设计理念,首堆示范工程电功率 116.1 万千瓦,
设计寿命 60 年
CP300 指 中核集团自主设计的 30 万千瓦的压水堆技术
CP600 指
中核集团在吸收国际压水堆技术的基础上,自主设计的 60 万千瓦二
代改进型压水堆技术
CP1000 指
中核集团在吸收国际压水堆技术的基础上,自主设计的 100 万千瓦
二代改进型压水堆技术
VVER-1000 指
俄罗斯设计准三代压水堆技术,设置双层安全壳、堆芯捕集器,电功
率 100 万千瓦,设计寿命 40 年
VVER-1200 指
俄罗斯设计的三代压水堆技术,设置双层安全壳、堆芯捕集器,采用
“能动与非能动”相结合的安全设计理念。电功率 120 万千瓦,设
计寿命 60 年
AP1000 指
西屋公司开发的三代压水堆技术,采用非能动安全设施和简化的电
厂设计,电功率 125 万千瓦,设计寿命 60 年
重水堆、
CANDU-6 指
加拿大设计的以重水作为慢化剂和冷却剂、天然铀为燃料、采用不
停堆更换燃料的反应堆技术,电功率 70 万千瓦,设计寿命 40 年
玲龙一号 指
以我国现有压水堆设计为基础,采用一体化反应堆技术路线,以热、
水、电多用途为目标,安全性可达到第三代核能系统技术水平的一体
化小型压水堆(简称 ACP100)。电功率 12.5 万千瓦,设计寿命 60
年
核电设备利用
小时数 指
机组在统计期内的发电量除以机组装机容量,如统计期内有新机组
首次并网,则新机组的装机容量应折算,折算比例为该机组实际运
行小时数除以统计期日历小时数
能力因子 指
机组可用发电量与额定发电量的比值,用百分比表示,机组能力因
子反映核电厂在优化计划停堆活动和降低非计划能量损失方面管理
的有效性,全部机组的平均能力因子为各机组能力因子的算数平均
值
敏捷端新产业 指
指高新技术产业投资开发。强调技术自主,重研发,相对轻资产,可
快速进入领先梯队,重点孵化符合国家战略方向,市场前景广阔的
高新技术产业。
WANO 指
世界核电运营者协会(World Association of Nuclear Operators,
WANO),为 1985 年 5 月在莫斯科成立的非营利性、非政府的世界性
组织,联合世界范围内所有运行商用核电站的
中国核电分析
搞钱
小工厂是如何盈利的?
trie tree (字典树)
什么是字典树(rie tree)
字典树,英文名 trie。顾名思义,就是一个像字典一样的树。
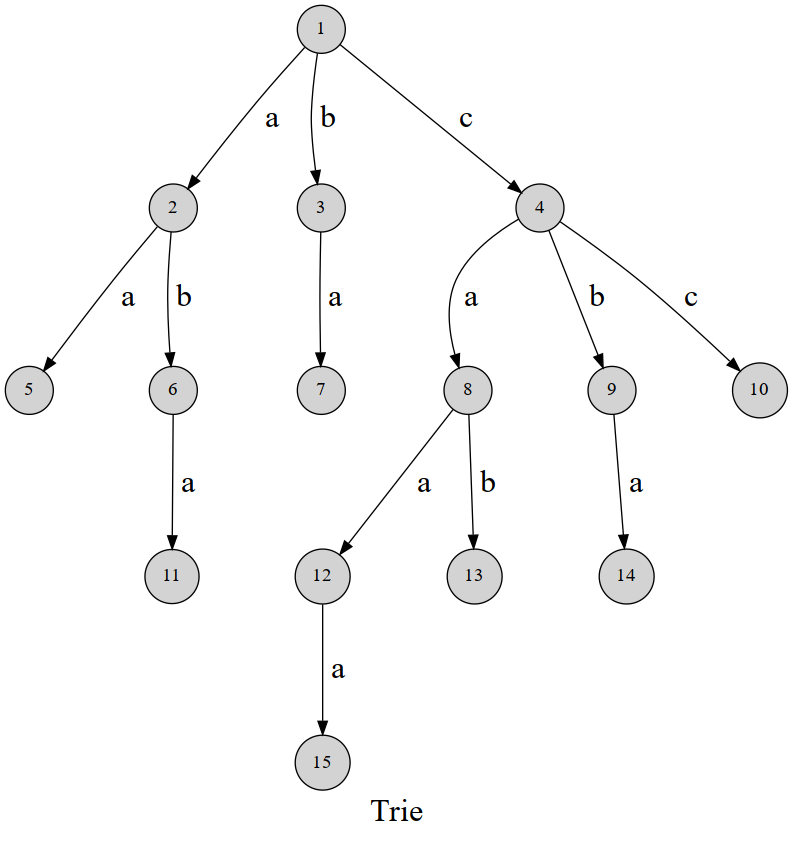
可以发现,这棵字典树用边来代表字母,而从根结点到树上某一结点的路径就代表了一个字符串。举个例子, 表示的就是字符串 caa。
trie 的结构非常好懂,我们用 $\delta(u,c)$ 表示结点 $u$ 的 $c$ 字符指向的下一个结点,或着说是结点 $u$ 代表的字符串后面添加一个字符 $c$ 形成的字符串的结点。
有时需要标记插入进 trie 的是哪些字符串,每次插入完成时在这个字符串所代表的节点处打上标记即可。
代码模板
1 | class Trie { |
trie tree 的应用
- 检索字符串
字典树最基础的应用——查找一个字符串是否在“字典”中出现过。 - AC 自动机
trie 是 AC 自动机 的一部分。 - 维护异或极值
将数的二进制表示看做一个字符串,就可以建出字符集为 的 trie 树
